It’s hard to believe this paper was not written ironically. Perhaps I am missing the author’s sense of dry humor? In a paper entitled Principal Component Analysis of Time Variations in the Mean-Variance Efficient Frontier, author Andreas Steiner subjects mean-variance optimization to principal component analysis, a mathematical way to determine the relative importance of factors. He extracted three important factors that determine the efficient frontier. The three factors together explained 99% of the shape of the efficient frontier.
In fact—and this is the funny part to me-one factor explained 95% of the shape of the efficient frontier. And what was that magic factor?
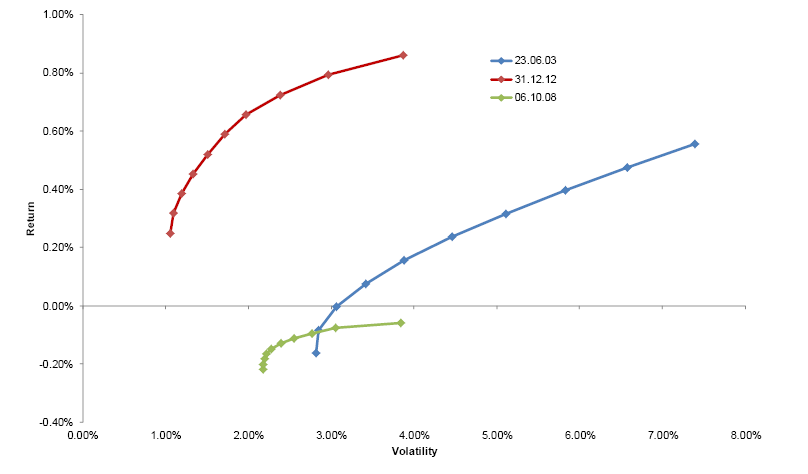
It was the level of returns. In other words, the shape of the efficient frontier depends on the returns of the various assets. If you can predict the returns, you will (mostly) know the shape of the efficient frontier. And, in case you were wondering, the shape of the efficient frontiers varies enormously depending on the time period. Below, for example, is a clip from the paper showing efficient frontiers calculated from trailing data at different times. I’m sure you can see the slight problem—the curves look nothing alike.
Source: Andreas Steiner/SSRN (click on image to enlarge)
The author writes:
We find that the level factor is highly correlated with average asset returns.
We interpret this result as evidence that successful investment management is mainly driven by return estimates and not “risk management” as has been in the spotlight since the Financial Crisis.
Here’s the immediate question that occurs to my feeble brain, although I’m guessing most 5th graders would be right there with me: If I could predict the return of each asset, why would I need an efficient frontier? Wouldn’t I just buy the best-performing asset?
Indeed, risk management is no big deal if I simply predict all of the asset returns. We’ve discussed many times before that mean-variance optimization is highly dependent upon returns, although correlations and standard deviation play a supporting role. All of these factors are moving targets, none more so than returns. Mean variance optimization, in practice, is a complete bust because obviously no one can reliably and consistently predict returns.
This kind of study—although mathematically rigorous—is silliness of the first degree. It reminds me certain academic follies, like the professors who wondered if monkeys at typewriters really could reproduce the works of Shakespeare. (The short answer is “no.”)
Modern portfolio theory would be relatively harmless if it remained in academia. However, when investors try to use it to build portfolios, it has the potential to cause a lot of damage. Although it is simply another theory that does not work in practice, it is enshrined in many finance textbooks and still taught to budding practitioners. Is it any wonder that we prefer tactical asset allocation driven by relative strength to guessing at future returns?
HT to CXO Advisory